Time complexity and space complexity in data structures and algorithms

at the present time, do you know, What is Time complexity and space complexity in data structures and algorithms?

with this in mind, let me explain to you what do we mean by time complexity and space complexity

in reality, for analyzing an algorithm we usually use  two parameters know as time and space to measure the efficiency of an algorithm

in essence, time and space are the scariest resources that we have

So, we should use it wisely to produce efficient results with speed

For example: Suppose you are given the task of transferring media files to some other country

in sum, what will you do?

You might say, you will transfer it through the internet but the problem is that the file is large (20TB) terabytes and you have internet with a bandwidth (transfer rate of 1000 Mbps)

to sum up, how much time will it take to transfer through the internet?

in reality, it will take 2days and 52 minutes, 2 seconds

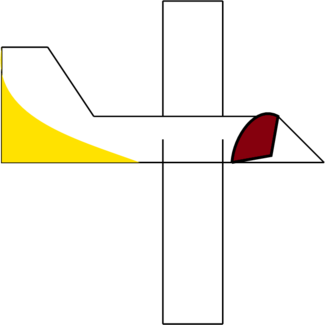
If it is urgent and you don’t mind cost then it would be better to transfer files through aircraft

So, that it will be delivered within a few hours to the desired  destination

To sum up: big O notation is a way to describe the algorithmic complexity of a function for a given  n amount of input 

Time complexity means if the time to run the function increases then it is called time complexity

Space complexity means if the memory to run the function increases then it is called space complexity

How to describe the runtime of an algorithm

in a word, we can describe the runtime of an algorithm by using a big O OR asymptotic notations

Remember  in essence, Big O  is an equation that describes how time changes to certain input

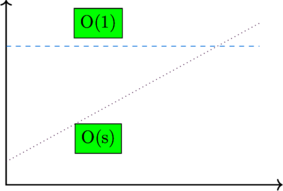
on the whole, for internet transfer:  we can describe the runtime of  a data transfer algorithm as O(s) where  ‘s’ is the size of the media file

in short, the time to transfer media file increases  linearly with the size of the file

for aircraft transfer: we can describe the runtime of a data transfer algorithm as O(1) because the time will remain constant no matter how much the size increase

Note: you should not have to use O(n) in every equation that,  you write, instead you can use  other variables such as O(s)

for (int i=0;i<b;;i++)
{
sum +=a;
}

For example, for the loop shown above, we can write runtime of it as O(b) instead of O(n)

Always the linear will surpass the constant at some point even the constant so big or how slow might the linear growth

Why we use time and space complexity

• Time and space complexity gives you an estimation so, that you won’t get shocked when the result is produced
• It produces a choice to select one of the two ways of doing something
• You will know, which part of the code should be optimized to utilize the resources efficiently

How to express time and space complexity

in brief, we can express time and space complexity by using a function called f(n)

without a doubt, where n is the size of the input

to sum up, the function f(n) is expressed by using the big O notation

At the same time, with time and space complexity, we would also like to predict the complexity of the algorithm as input size increases

at this point, the below graph show’s the rate of growth of some famous big O times

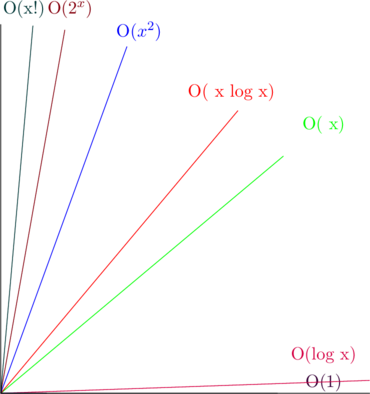
So, that means O(1) has the least complexity while O(x!) has the highest complexity

Space complexity

in a word, space complexity means the space or memory which is required by the algorithm to run efficiently

in contrast, the space complexity is a parallel concept to time complexity

For example: to iterate an array from 0 to n it will take time complexity O(n) and space  complexity O(n) space

For two dimensional array such as a matrix of order nxn it will take time complexity of O() and space complexity O() space

What causes a space complexity in a function?

1. Variables
2. Data structures
3. Function call
4. Memory allocations

Some basics rules of big O

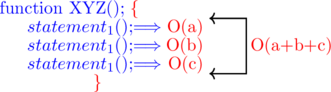
#Rule 1: Add different statements runtime

in this situation, to find the runtime of a code snippet  we should add all the statements runtime

#Rule 2:Neglect the constant

to begin with, consider the two code snippet mentioned below for finding the min and max element in an array

this time, the first code snipped contain two loops for doing the same work as the second code snipped

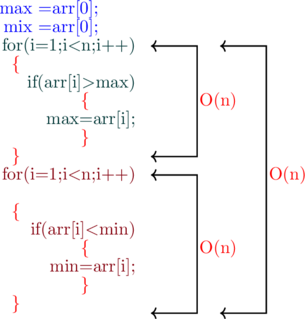
on this occasion, the Second code snipped contain only one loop with two instruction to the same job as first code snipped

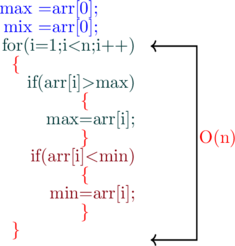
So, what do you think?

at this time, which  code snipped will run faster?

on the contrary, do you know, both the code snippets will take the same time to run the code

But, why?

on one hand, always remember you should neglect the constant for finding the run time of the algorithm

You might say the first code snipped contain two loops so, it will take run time as O(n)+O(n)=O(2n)

to sum up, No!, it won’t!

we neglect the constant and write O(n) instead of O(2n) also don’t think that by writing O(2n) you are more precise

in this situation, No!, you are not!

#Rule 3:Neglect the non-dominant terms

at this time, let us consider, a code snippet as mentioned below

by all means, the first part of the code is to find a max element in an array which take O(n) run times

by and large, the second part of the code is to iterate an arrays by a and b and print all the elements  O()

As we said, we should neglect the constants but what if we have an expression like this O( +n), then  here n is not exactly a constant

as a matter of fact, what will you do?

You should also neglect the non-dominant terms in a big O expression

When it comes to big O notation, we usually care about significant terms that have the most impact, and also, remember, as the input grows larger then at that instant only the fastest growing terms matter most than constants

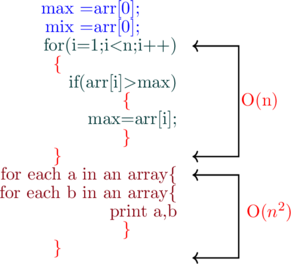
Consider some examples

• O()  gives  O()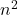

• O(n+log n) gives O(n)

• O(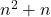) gives O()

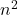• O(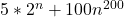) gives O()

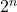Note: the expression O() cannot be reduced until you have some specific knowledge about it

#Rule 4: different inputs gives different variables

at this point, consider the two code snippets first and second as mentioned below

Most people would get confused here, at this instant, they would say both, they find codes snipped are similar so, therefore it is O()

undoubtedly, No, it is not!

Remember  when n is the size of the array, if the code snipped have two different arrays then it does not mean  the length of the entire array

Constant time

Suppose, we are having a simple C program to print Hi there! Then how time much will it take to execute the print statement, it will take constant time to execute the print statement

 in sum, the constant time does not depend on the input size

#include <stdio.h>
int main()
{
    printf("Hi there!\n");
    return 0;
}

to clarify, the above program is having O(1)

at this time, where O is called  “order of”

Linear loops (Single loop)

Suppose, we have an Array of size 10 and we would like to iterate all the elements of a given array, then, in that case, how much time will it take to iterate all the elements of an Array?

 for(i=0;i<9;i++)
    {
     printf("%d\n",arr[i]);
    }

It usually, depends upon, how many elements are there in an array suppose, if we have n elements in an array then, in that case, the time taken will be O(n)

 for(i=0;i<9;i+=2)
    {
     printf("%d\n",arr[i]);
    }

On the other hand, if we iterate half of the loop then at that instant, the time taken will be O(n/2)

after all, with every iteration in linear loops you can ADD or SUB

Logarithmic loops

after that, with every iteration in Logarithmic loops, you can Divide or Multiply

Case 1

for(i=1;i<9;i=i*2)
    {
     printf("%d\n",arr[i]);
    }

Case 2

 for(i=9;i>=1;i=i/2)
    {
     printf("%d\n",arr[i]);
    }

at this instant, the time taken by logarithmic loops will be O(log n)

Nested loops

in a word, a loop that contains loops inside it, is called a nested loop

Linear logarithmic loops

for(i=0;i<10;i++)
    for(j=1;j<10;j*=2)
 {
          statements;
      }

this time, every iteration of the inner loop is multiplied by 2

so far, the time taken by linear logarithmic loops to executed the statements is given as O(n log n)

Quadratic loop

to sum up, in a quadratic loop, every iteration of the outer loop is equal to every iteration of the inner loop

for(i=0;i<10;i++)
    for(j=0;j<10;j++)
 {
          statements;
      }

so far, the time taken by the quadratic loop is given by O()

Dependent quadratic loop

thereafter, in a dependent quadratic loop, the inner loop will be dependent on the outer loop

for(i=0;i<10;i++)
    for(j=0;j<=1;j++)
{
    statements
}

thus, the time taken by the dependent quadratic is given by O(n+1)/2

Cubic loop

Case 1

for(int i = 0; i < 10; i++)
  for(int j = 0; j < 10; j = j + +)
    for(int k = 0; k < 10; k = k + +)
      {
          statements;
      }

Case 2

for(int i = 0; i < 10; i++)
  for(int j = 0; j < 10 + 5; j = j + 2)
    for(int k = 0; k < 10; k = k + 3)
      {
          statements;
      }

similarly, the time taken by the three loops will be given by O()

O(n!)

Let’s talk about a big O that you won’t likely encounter in case, if you are writing some code  and you have O(n!) complexity then that means you are doing something wrong

You probably won’t  encounter it but it exists

void nFacRuntimeFunc(int n){
for(int i=0; i<n; i++){
nFacRuntimeFunc(n-1);
}
}

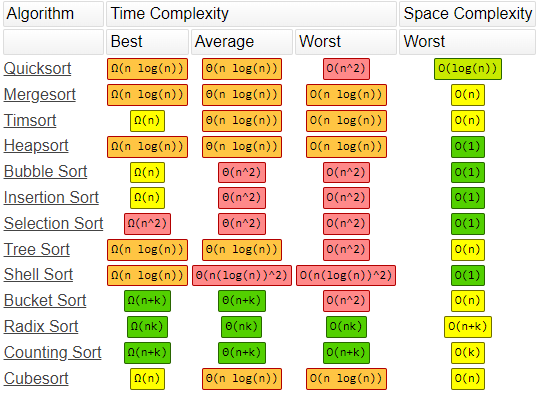
Array sorting Algorithms

Some BIG O calculation examples

at this point, to do some BIG O calculations let’s use some JavaScript examples as mentioned below

 Suppose, we have a function called one that has two statements that are  of O(1) and, O (1), and also a loop that contains another function called two that is outside the function one

As we know, always a for loop will be linear, so, O(n) while, the function called two is dependent upon the input size so, O(n)

Next, consider a random statement (let stranger =true;)that will get executed as many times as the input size so, O(n) then the statement a++; is also in the loop so, O(n)

function one(input) {
let a=10; //O(1)
a=60+33; // O(1)
for(let i=0; i<input.length; i++){ //O(n)
functiontwo(); //O(n)
let stranger =true; //O(n)
a++;   //O(n)
}
return a; // O(1)
}
one() //function call

O(1)+ O(1)+ O(1)+ O(n)+ O(n)+ O(n)+ O(n)

3+4n

BIG O(3+4n) =n

So, BIG O(n)

function one(input){
let a=20; //O(1)
let b=75; //O(1)
for(let i=0; i < input; i++){
let x=i+2;  //O(n)
let y=i+4;  //O(n)
let z=i+2;   //O(n)
}
for(let j=0; j<input; j++){
let c= j*2;  //O(n)
let d= j*3;  //O(n)
}
let status ="random"; //O(1)
}

BIG O(3+5n)=n

So, BIG O(n)

function sketch(items){
    console.log(item[0]);
var middleIndex =Math.floor(items.length/2);
var index =0;
while (index< middleIndex){
    console.log(items[index]);
    index++;
}
for (var i=0; i< 100; i++){
    console.log('hi');
    }
}

The above function sketch first, print the first item in the array so, O(1) then, print half of the array items by using a while loop so, O(n/2) next, we are not looping all the items in the array but instead, we loop only 100 items by using a for loop

O(1)+O(n/2)+O(100)

O(1+n/2+100)

O(n/2+100)

BIG O(n)

function printAllNumbersThenAllPairSums(numbers) {
  console.log('these are the numbers:'); 
  numbers.forEach(function(number) {   //O(n)
    console.log(number);
  });
  console.log('and these are their sums:');
  numbers.forEach(function(firstNumber) {     //O(n)
    numbers.forEach(function(secondNumber) {  //O(n)
      console.log(firstNumber + secondNumber);
    });
  });
}
printAllNumbersThenAllPairSums([1,2,3,4,5])

O(n)+O(n) X O(n)

O(n)+O()

O(n+)

Use the rule #3

BIG O()

Let us suppose, we have a function called print all numbers then all pair sums

In the first part of the code, print all the numbers in an array that is of O(n)

The second part of the code, contains two for loops that are of O() also it add the numbers in an array in serial order such as [1+1, 2+1, 3+1, 4+1, 5+1][2+1, 2+2, 3+2, 4+2, 5+2].. etc.

The big O notation of the function called print all numbers then all pair sums is O(n+)

The purpose of the rule#3 is to neglect the non dominant terms which mean we care only about the most important term, in this case, we neglect the O(n)

But, Why?

Because as the input increases the size of the is more important than O(n)

So, that means we always keep the most dominant term

Let’s see, another example to make the rule #3 clear

for instance, suppose, we have a BIG O(+5n+200+n/2)

on this occasion, how do we simplify the above BIG O by using rule #3?

As we know, the  rule#3 says we only worry about the most dominant term because the term increases most rapidly than any other term in the BIG O

So, we can write BIG O() by dropping the all non- dominant terms

Some space complexity examples

Let’s suppose, we have a function called Demo that prints out “hi there” 5 times  then the time complexity of that function will be O(n) and space complexity will be O(1)

But, why the space complexity is O(1) here?

Because The only thing the demo function is doing is creating a variable called let i=0;

finally, that’s it, We are not adding any additional items to the memory

function demo(n) {
    for (let i = 0; i < n; i++) { //O(1) space and //O(n) Time
        console.log('hi there');
    }
}
demo(5); // function call with parameter

Let’s consider another simple function called Demo that prints “hi” 6 times then the time complexity will be O(n) and space complexity will be O(n)

But, why the space complexity is O(n) here?

Because we created an array and fill it with the item “hi” and we also created a variable  but as per our big O rule #2 we neglect the constants so, it will be O(n)  

function Demo(n) {
    var array = []; //O(n) space
    for (let i = 0; i < n; i++) { // O(n) Time
        array[i] = 'hi';
    }
    console.log( array);
}
Demo(6) //function call