understanding recursion concept
Recursion means a function call, which calls itself repeatedly until it terminated by its base condition
Always recursion should have a base condition so, that it won’t fall into an infinite loop
If the base condition is false then the recursion loop will be terminated and if the base condition is true then it will make recursive calls till the base condition becomes false
Remember: you will find recursion a little bit harder to understand than iteration
The things which you can do with recursion you can also do with stack and iteration
It is always better you consider alternative approaches before using recursion

Recursion is useful for the searching and sorting algorithms and also it is a common topic in interviews
Anything done with recursion can also be done with iteration(loop)
If that is true! Then why should we use a confusing concept called recursion?
Because, in programming there will be always pros and cons so, being a software developer you need to make the right decisions based on pros and cons
Iterative approaches, tend to be more efficient because they don’t add any additional stack layer for every function call they made
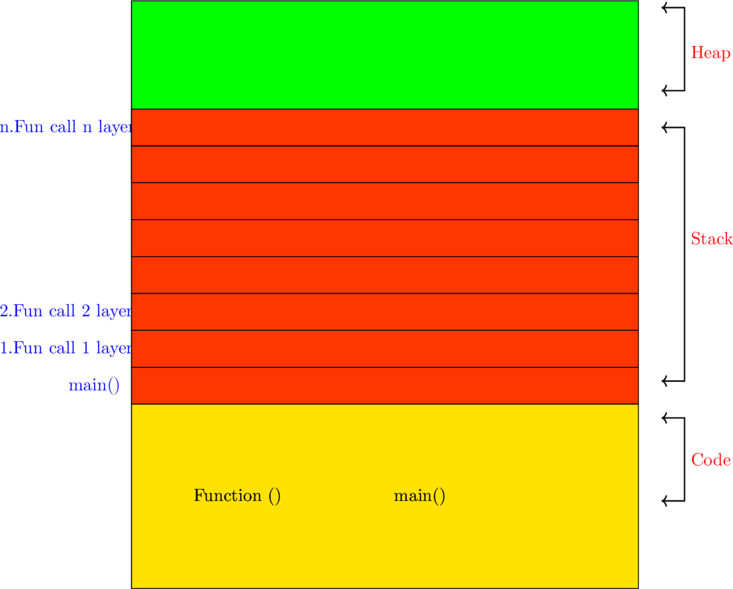
Stack overflow
As you might know, the memory is a limited resource and that is divided into three section
- code section
- stack section
- heap section
stack overflow means when a function call that, falls into an indefinite loop so, because, of that, the program will run out of memory and crashes
recursive algorithms can be very space inefficient because they create a new stack layer for every recursive call
Recursion will have two-phases
- Calling phase
- Returning phase
Calling Phase
Consider a simple C example
The below example shows that the function is taking parameter n and checking the condition whether n>0, if the base condition is true then it will print n and call itself
#include <stdio.h>
void function(int n)
{
if(n>0)
{
printf("%d",n);
function(n-1); // O(n) Time and O(n) space
}
}
int main()
{
int x=5;
function(x);
return 0;
}Output
54321Let’s analyze the time complexity of the above function which is O(n) and the space complexity will also be O(n)
Why the space complexity is O(n) here?
Because each recursive call will add a new layer to the stack, if it made 2 recursive calls then it will add 2 new layers to the stack and in case, if it is made n recursive call then it will add n new layers to the stack
Tracing the recursive function
Recursive functions are always traced in the form of a tree
Here first it has to print and then call itself till it reaches condition (1-1)
Note: the printing is done at the calling time

Let’s implement the calling phase through a loop
#include <stdio.h>
void function(int n)
{
int i;
for(i=n;i>0;i--)
{
printf("%d",i);
}
}
int main()
{
int x=5;
function(x);
return 0;
}Output
54321#include <stdio.h>
void function(int n)
{
while(n>0)
{
printf("%d",n);
n--;
}
}
int main()
{
int x=5;
function(x);
return 0;
}Output
54321Let’s analyze the time complexity of the above function which is O(n) and the space complexity will also be O(1)
Note: if you would like to write a calling phase function then it would be better to convert it to a loop because it will be more efficient when it comes to space but this will not be the same for every type of recursion or loop
Returning Phase
#include <stdio.h>
void function(int n)
{
if(n>0)
{
function(n-1);
printf("%d",n);
}
}
int main()
{
int x=5;
function(x);
return 0;
}Output
12345Tracing the recursive function
From the main function calling the function by passing a value of 5 then it will call itself by (5-1),(4-1),(3-1), and (2-1) till it reaches (1-1) condition where it will get terminated
Once the function gets terminated then at that instant, the function will go to the previous call (1-1) and print 1 similarly, it will call itself till it reaches (5-1) and print 5
Note: the printing is done at the returning time

Let’s implement the returning phase through a loop
If a recursive function has to do something at returning phase then it would be difficult to convert it to iterative form but it can be converted
#include <stdio.h>
void function(int n)
{
int i;
for(i=1;i<=n;i++)
{
printf("%d",i);
}
}
int main()
{
int x=5;
function(x);
return 0;
}Output
12345#include <stdio.h>
void function(int n)
{
int i=1;
while(i<=n)
{
printf("%d",i);
i++;
}
}
int main()
{
int x=5;
function(x);
return 0;
}Output
12345Difference b/w calling time and returning time
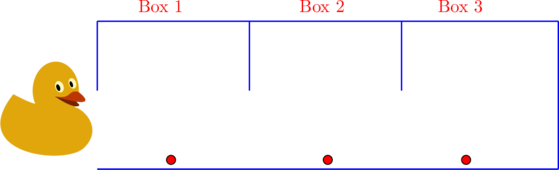
Let us suppose we have a duck house that have three boxes with one rice seed in each box
calling time
Assume, that you have instructed the duck to perform two steps as mentioned below recursively
- Eat the rice seed(perform the task)
- Move to the next box(recursive call)
First, the duck will eat the rice seed in the Box1, second, the duck will move to the BOX2 then the duck will eat the rice seed in the Box2 and will move to Box3, finally, it will eat the rice seed in the Box3
O/P: 1 2 3
So, the duck is eating rice when moving forward
returning time
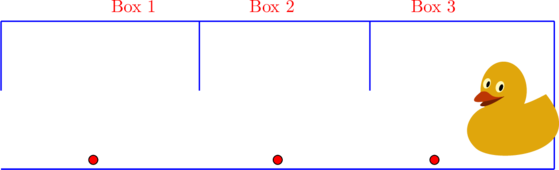
Assume, that you have instructed the duck to perform two steps as mentioned below recursively
- Move to the next box (recursive call)
- Eat the rice seed (perform the task)
First, the duck will move to Box1 second, the duck will move to Box2 third, the duck will move to Box3 fourth, it will eat the rice seed from Box3 fifth, it will move to Box2 and it will eat the rice seed from the Box2 and finally, it will move to Box1 and will eat the rice seed in the Box1
O/P: 3 2 1
So, the duck will be eating rice during returning phase
In a recursion function if any thing is there before the recursive call then that statement will be executed at the calling time(Ascending) and if the statement is present after the recursive call then that statement will be executed at the returning time(descending)
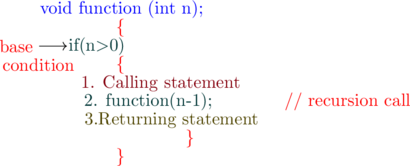
#include <stdio.h>
void function(int n)
{
if(n>0)
{
printf("%d",n);
function(n-1);
printf("%d",n);
}
}
int main()
{
int x=5;
function(x);
return 0;
}Output
5432112345Tree recursion
If a recursive function calls itself more than once then it is called a tree recursion
#include <stdio.h>
void function(int n)
{
if(n>0){
printf("%d", n);
function(n-1);
function(n-1);
}
}
int main() {
function(4);
return 0;
}Output
432112113211211The time complexity for the above tree recursive function is O(![]() ) and the space complexity is O(n)
) and the space complexity is O(n)
A small practical example of recursion
Let’s suppose, you have a laptop and you would like to search a file called assignment_operator.cpp from the desktop but the problem is that you can not find an assignment_operator.cpp program in a single folder, so, to find the file, you need to search folders recursively
Let us see what do I mean?
If you have a Linux operating system then you can use the below commands to search a specific file in your system
To list all the folders
lsTo access a specific folder
cdYou can also see it here, in the Anees-workspace directory i have a folder called assignment_operator
ls -Rhere, in the above command, R stands for recursion by using the above command we can view the files inside a folder
A practical example for recursion
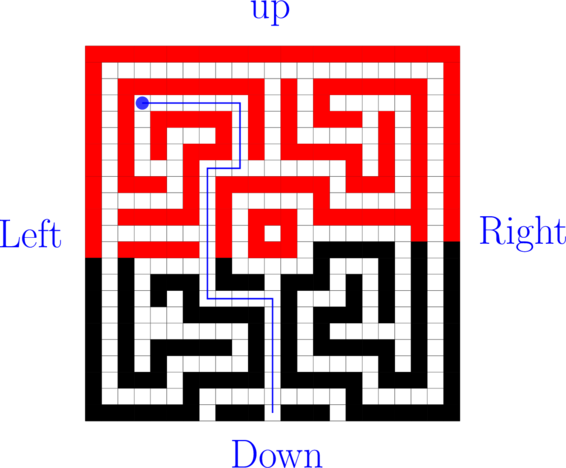
Consider a C++ program for finding the way through the maze
A maze is a grid and at each point, you can move left, right, down, up to find the way out of the maze
if we use recursion, then we can start at the beginning and move left, right, up down to find the way out of the maze
notice find_the_path function is recursively used
bool find_the_ path(maze,point_location)
//check it is already tried
if(already_visited(maze,location))
{
return false;
}
// check if this position is exit
if(the_exit(maze,location))
{
return true;
}
//recall the position which has been tried
recall_position(maze,location)
if(move_right(maze,location,&new_location)){
if(find_the_path(maze,new_location))
{
return true;
}
}
if(move_up(maze,location,&new_location)){
if(find_the_path(maze,new_location)){
return true;
}
}
if(move_down(maze,location,&new_location)){
if(find_the_path(maze,new_location)){
return true;
}
}
if(move_left(maze,location,&new_location)){
if(find_the_path(maze,new_location)){
return true;
}
}
return false;
}Sum of n natural numbers
#include <stdio.h>
#include <stdlib.h>
void add(int n)
{
int i;
int sum=0;
for(i=0;i<=n;i++) //O(n) Time and O(1) space
{
sum=sum+i;
}
{
printf("%d",sum);
}
}
int main()
{
int x=5;
add(x);
return 0;
}Output
15Sum of n natural numbers by using recursion
#include <stdio.h>
int function(int n)
{
{
if(n==0)
return 0;
else
return function(n-1)+n; // O(n) Time and O(n) space
}
}
int main()
{
int x=5;
int sum;
sum=function(x);
printf("%d",sum);
return 0;
}
15Sum(5)=15
Sum(4)+5=10+5=15
Sum(3)+4=6+4=10
Sum(2)+3=3+3=6
Sum(1)+2=1+2=3
Sum(0)+1=0+1
As you can see, from the above recursive tree that the addition is done while returning
similarly, the height of the stack of the above function is 6 because it made 6 recursive calls so, for n calls the space complexity will be O(n)
Factorial
n!=n*(n-1) n*(n-2) n*(n-3) n*(n-4) n*(n-5)……….3*2*1
so, that means n goes till it reaches value 1
n!=n*(n-1)!
8!=8*(7-1)!=8*7!
6!=1*2*3*4*5*6=720
0!=1
1!=1
Factorial using recursion
As you can see, the sum of n natural numbers and factorial are similar but in the sum of n natural numbers we did the addition fac(n-1)+n and for factorial, we did multiplication fac(n-1)*n
For the multiplication of factorial, we use 1 instead of 0 because if we multiple anything with 0 will also become 0
#include <stdio.h>
int function(int n)
{
{
if(n==0)
return 1;
else
return function(n-1)*n; // O(n) Time and O(n) space
}
}
int main()
{
int x=6;
int fac;
fac=function(x);
printf("%d",fac);
return 0;
}Output
720Factorial with iteration
#include <stdio.h>
#include <stdlib.h>
void Fac(int n)
{
int i;
int fac=1;
for(i=1;i<=n;i++) //O(n) Time and O(1) space
{
fac=fac*i;
}
{
printf("%d",fac);
}
}
int main()
{
int x=6;
Fac(x);
return 0;
}Output
720Calculate exponents
![]() = 2*2*2*2=16
= 2*2*2*2=16
To calculate exponents we can use a library called <math.h> and the <math.h> library have a function called pow() to calculate exponents
Pow(2,4)=![]()
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
int p;
p=pow(2,2);
printf("%d",p);
return 0;
}Output
4Calculate exponents by using recursion
#include <stdio.h>
int power(int x, int y)
{
if(y==0)
return 1;
else
{
return power(x,y-1)*x;
}
}
int main()
{
int p;
p=power(2,2);
printf("%d",p);
return 0;
}Output
4Calculate exponents iteratively
#include <stdio.h>
void power(int m, int n)
{
int i;
int p=1;
for(i=1;i<=n;i++)
{
p=p*m;
}
{
printf("%d",p);
}
}
int main()
{
power(2,6);
return 0;
}Output
64Fibonacci numbers
Fib(n) can be defined as by recursive formula fib(n-2)+fib(n-1) where n>1 as well as by setting the values such as if n=0 then it will be 0 and if n=1 then it will be 1
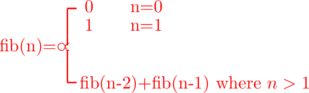
Every term in Fibonacci numbers is obtained by adding previous two terms but at least should have two initial terms
For example, fib(8) means an addition of 4th term(3) and 5th term(5)
| Fib(n) | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
|---|---|---|---|---|---|---|---|---|
| n | 0th term | 1st term | 2nd term | 3rd term | 4th term | 5th term | 6th term | 7th term |
Fibonacci numbers by using recursion
#include <stdio.h>
int fib(int n)
{
{
if(n==0)
return 0;
if (n==1)
return 1;
else
return fib(n-1)+fib(n-2);
}
return 0;
}
int main()
{
int x=7;
int f;
f=fib(x);
printf("%d",f);
return 0;
}Output
13As you can see from the above function the 7th term of the Fibonacci series is 13
The time complexity of the above function is ![]()
Why it is ![]() ?
?
Because when we have a function and that function is calling two times then that means it is ![]()
Usually, when we use two loops such as a quadratic loop
for(i=0;i<10;i++)
for(j=0;j<10;j++)
{
statements;
} the time taken quadratic loop is given by ![]()
Fibonacci numbers by using iteration
#include <stdio.h>
int fib(int n)
{
int to=0, t1=1, sum;
if(n<=1)
return n;
for(int i=2;i<=n;i++) //the loop starts from 2 and reaches the n
{
sum=to+t1;//Find the sum by adding two terms
to=t1; //replace the value t1 with t0
t1=sum; //replace the value of t1 with the sum
}
return sum;
}
int main()
{
int x=7;
printf("%d",fib(x));
return 0;
}Output
13The time complexity for the iterative function is O(n)
The logic
to t1 sum
0 + 1 1
1 + 1 2 replace t0 with t1 and t1 with sum then repeat the same process
1 + 2 3
2 + 3 5
3 + 5 8
The O/P: 0 1 1 2 3 5 8
Dynamic programming
Dynamic programming means taking a recursive algorithm and finding the excessive calls(overlapping subproblems) and storing the results of the function so that it can be utilized again when needed
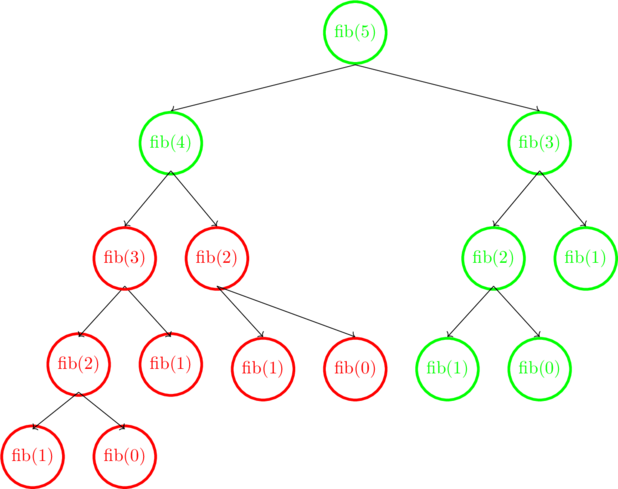
Recursion tree of Fibonacci numbers
The below figure shows the recursion tree of fib(5) and it had made 15 calls
The red color calls are the excessive calls that the fib(5) had made
Excessive calls are the recursion function calls that call themselves multiple times for the same values such as (recursive implementation of Fibonacci numbers)
Memoization
Memoization(remember) and reuse solutions to sub-problems so, that to solve the problem
To avoid excessive calls by retaining values to be utilized for future calls we can use the static variable or global variable
On the other hand, by storing the results of the function calls in an array so, that they can be utilized again when we need the same call
In other words, by storing the result in an array we have reduced the excessive calls
![]()
Initialize the array with -1 and -1 means we don’t know the value
Therefore, by using the memorization approach we have reduced the time complexity of Fibonacci numbers from O(![]() ) to O(n)
) to O(n)
#include <stdio.h>
int F[20]; //Create a global array of size 20
int fib(int n)
{
if(n<=1)
{
F[n]=n;//If n<=1 then store the value of n in F[n]
return n;
}
else{
if(F[n-2]==-1)//check if f[n-2]==-1
F[n-2]=fib(n-2);//call the function fib(n-2) and store the result in f[n-2]
if(F[n-1]==-1);
F[n-1]=fib (n-1);
return F[n-2]+F[n-1];//return the stored result
}
}
int main()
{
int i;
int x=7;
for(i=0;i<20;i++)
F[i]=-1; //initialize the whole array with -1 because 0 is also a Fibonacci term
printf("%d",fib(x));
return 0;
}Output
13

Leave a Reply