800+ LaTeX symbols α,β,γ,δ

Use the amssymb and amsmath package to create symbols in LaTeX

\usepackage{amssymb,amsmath}

Text-mode Commands

Caution! Caution! Don’t use this command in math mode, such as $\textbf{\textdollar \textdollar}$

but why?

because, these are the text-based command but if you like to use math mode then use $\textbf{\textdollar }$ \textbf{……} $\textbf{\textdollar }$

$\textbf{\textasciicircum }$
\textasciicircum

$\textbf{\textasciitilde}$
\textasciitilde

$\textbf{\textasteriskcentered}$
\textasteriskcentered

$\textbf{\textbackslash}$
\textbackslash

$\textbf{\textbar}$
\textbar

$\textbf{\textbardbl}$
\textbardbl

$\textbf{\textbigcircle }$
\textbigcircle

$\textbf{\textbraceleft}$
\textbraceleft

$\textbf{\textbraceright}$
\textbraceright

$\textbf{\textbullet}$
\textbullet

$\textbf{\textcopyright}$
\textcopyright

$\textbf{\textdagger}$
\textdagger

$\textbf{\textdaggerdbl}$
\textdaggerdbl

$\textbf{\textdollar}$
\textdollar

$\textbf{\textellipsis}$
\textellipsis

$\textbf{\textemdash}$
\textemdash

$\textbf{\textendash}$
\textendash

$\textbf{\textexclamdown}$
\textexclamdown

$\textbf{\textgreater}$
\textgreater

$\textbf{\textless}$
\textless

$\textbf{\textordfeminine}$
\textordfeminine

$\textbf{\textordmasculine}$
\textordmasculine

$\textbf{\textparagraph }$
\textparagraph

$\textbf{\textperiodcentered}$
\textperiodcentered

$\textbf{\textpertenthousand}$
\textpertenthousand

$\textbf{\textperthousand}$
\textperthousand

$\textbf{\textquestiondown}$
\textquestiondown

$\textbf{\textquotedblleft}$
\textquotedblleft

$\textbf{\textquotedblright}$
\textquotedblright

$\textbf{\textquoteleft}$
\textquoteleft

$\textbf{\textquoteright}$
\textquoteright

$\textbf{\textregistered}$
\textregistered

$\textbf{\textsection}$
\textsection

$\textbf{\textsterling}$
\textsterling

$\textbf{\texttrademark}$
\texttrademark

$\textbf{\textunderscore }$
\textunderscore

$\textbf{\textvisiblespace}$
\textvisiblespace

Symbols

$\imath$
\imath

$\jmath$
\jmath

$\|$
\|

$\backslash$
\backslash

Greek letters

$\Gamma$
\Gamma

$\Delta$
\Delta

$\Lambda$
\Lambda

$\Phi$
\Phi

$\Pi$
\Pi

$\Psi$
\Psi

$\Sigma$
\Sigma

$\Theta$
\Theta

$\Upsilon$
\Upsilon

$\Xi$
\Xi

$\Omega$
\Omega

$\alpha$
\alpha

$\beta$
\beta

$\gamma$
\gamma

$\delta$
\delta

$\epsilon$
\epsilon

$\zeta$
\zeta

$\eta$
\eta

$\theta$
\theta

$\iota$
\iota

$\kappa$
\kappa

$\lambda$
\lambda

$\mu$
\mu

$\nu$
\nu

$\xi$
\xi

$\pi$
\pi

$\rho$
\rho

$\sigma$
\sigma

$\tau$
\tau

$\upsilon$
\upsilon

$\phi$
\phi

$\chi$
\chi

$\psi$
\psi

$\omega$
\omega

$\digamma$
\digamma

$\varepsilon$
\varepsilon

$\varkappa$
\varkappa

$\varphi$
\varphi

$\varpi$
\varpi

$\varrho$
\varrho

$\varsigma$
\varsigma

$\vartheta$
\vartheta

Alphabetic symbols

$\aleph$
\aleph

$\beth$
\beth

$\daleth$
\daleth

$\gimel$
\gimel

$\complement$
\complement

$\ell$
\ell

$\eth$
\eth

$\hbar$
\hbar

$\hslash$
\hslash

$\mho$
\mho

$\partial$
\partial

$\wp$
\wp

$\circledS$
\circledS

$\Bbbk$
\Bbbk

$\Finv$
\Finv

$\Game$
\Game

$\Im$
\Im

$\Re$
\Re

Miscellaneous symbols

$\blacktriangledown$
\blacktriangledown

$\blacktriangle$
\blacktriangle

$\#$
\#

$\&$
\&

$\angle$
\angle

$\backprime$
\backprime

$\bigstar$
\bigstar

$\blacklozenge$
\blacklozenge

$\blacksquare$
\blacksquare

$\bot$
\bot

$\clubsuit$
\clubsuit

$\diagdown$
\diagdown

$\diagup$
\diagup

$\diamondsuit$
\diamondsuit

$\emptyset$
\emptyset

$\exists$
\exists

$\flat$
\flat

$\forall$
\forall

$\heartsuit$
\heartsuit

$\infty$
\infty

$\lozenge$
\lozenge

$\measuredangle$
\measuredangle

$\nabla$
\nabla

$\natural$
\natural

$\neg$
\neg

$\nexists$
\nexists

$\prime$
\prime

$\sharp$
\sharp

$\spadesuit$
\spadesuit

$\sphericalangle$
\sphericalangle

$\square$
\square

$\surd$
\surd

$\top$
\top

$\triangle$
\triangle

$\triangledown$
\triangledown

$\varnothing$
\varnothing

Binary operator symbols

$*$
*

$+$
+

$-$
–

$\amalg$
\amalg

$\ast$
\ast

$\barwedge$
\barwedge

$\bigcirc$
\bigcirc

$\bigtriangledown$
\bigtriangledown

$\bigtriangleup$
\bigtriangleup

$\boxdot$
\boxdot

$\boxminus$
\boxminus

$\boxplus$
\boxplus

$\boxtimes$
\boxtimes

$\bullet$
\bullet

$\cap$
\cap

$\Cap$
\Cap

$\cdot$
\cdot

$\centerdot$
\centerdot

$\circ$
\circ

$\circledast$
\circledast

$\circledcirc$
\circledcirc

$\circleddash$
\circleddash

$\cup$
\cup

$\Cup$
\Cup

$\curlyvee$
\curlyvee

$\curlywedge$
\curlywedge

$\dagger$
\dagger

$\ddagger$
\ddagger

$\diamond$
\diamond

$\div$
\div

$\divideontimes$
\divideontimes

$\dotplus$
\dotplus

$\doublebarwedge$
\doublebarwedge

$\gtrdot$
\gtrdot

$\intercal$
\intercal

$\leftthreetimes$
\leftthreetimes

$\lessdot$
\lessdot

$\ltimes$
\ltimes

$\mp$
\mp

$\odot$
\odot

$\ominus$
\ominus

$\oplus$
\oplus

$\oslash$
\oslash

$\otimes$
\otimes

$\pm$
\pm

$\rightthreetimes$
\rightthreetimes

$\rtimes$
\rtimes

$\setminus$
\setminus

$\smallsetminus$
\smallsetminus

$\sqcap$
\sqcap

$\sqcup$
\sqcup

$\star$
\star

$\times$
\times

$\triangleleft$
\triangleleft

$\triangleright$
\triangleright

$\uplus$
\uplus

$\vee$
\vee

$\veebar$
\veebar

$\wedge$
\wedge

$\wr$
\wr

Relational symbols and variants

$<$
<

$=$
=

$>$
>

$\approx$
\approx

$\approxeq$
\approxeq

$\asymp$
\asymp

$\backsim$
\backsim

$\backsimeq$
\backsimeq

$\bumpeq$
\bumpeq

$\Bumpeq$
\Bumpeq

$\circeq$
\circeq

$\cong$
\cong

$\curlyeqprec$
\curlyeqprec

$\curlyeqsucc$
\curlyeqsucc

$\doteq$
\doteq

$\doteqdot$
\doteqdot

$\eqcirc$
\eqcirc

$\eqsim$
\eqsim

$\eqslantgtr$
\eqslantgtr

$\eqslantless$
\eqslantless

$\equiv$
\equiv

$\fallingdotseq$
\fallingdotseq

$\geq$
\geq

$\geqq$
\geqq

$\geqslant$
\geqslant

$\gg$
\gg

$\ggg$
\ggg

$\gnapprox$
\gnapprox

$\gneq$
\gneq

$\gneqq$
\gneqq

$\gtrapprox$
\gtrapprox

$\gtreqless$
\gtreqless

$\gtreqqless$
\gtreqqless

$\gtrless$
\gtrless

$\gtrsim$
\gtrsim

$\gvertneqq$
\gvertneqq

$\leq$
\leq

$\leqq$
\leqq

$\leqslant$
\leqslant

$\lessapprox$
\lessapprox

$\lesseqgtr$
\lesseqgtr

$\lesseqqgtr$
\lesseqqgtr

$\lessgtr$
\lessgtr

$\lesssim$
\lesssim

$\ll$
\ll

$\lll$
\lll

$\lnapprox$
\lnapprox

$\lneq$
\lneq

$\lneqq$
\lneqq

$\lnsim$
\lnsim

$\lvertneqq$
\lvertneqq

$\ncong$
\ncong

$\neq$
\neq

$\ngeq$
\ngeq

$\ngeqq$
\ngeqq

$\ngeqslant$
\ngeqslant

$\ngtr$
\ngtr

$\nleq$
\nleq

$\nleqq$
\nleqq

$\nleqslant$
\nleqslant

$\nless$
\nless

$\nprec$
\nprec

$\npreceq$
\npreceq

$\nsim$
\nsim

$\nsucc$
\nsucc

$\nsucceq$
\nsucceq

$\prec$
\prec

$\precapprox$
\precapprox

$\preccurlyeq$
\preccurlyeq

$\preceq$
\preceq

$\precnapprox$
\precnapprox

$\precneqq$
\precneqq

$\precnsim$
\precnsim

$\precsim$
\precsim

$\risingdotseq$
\risingdotseq

$\sim$
\sim

$\simeq$
\simeq

$\succ$
\succ

$\succapprox$
\succapprox

$\succcurlyeq$
\succcurlyeq

$\succeq$
\succeq

$\succnapprox$
\succnapprox

$\succneqq$
\succneqq

$\succnsim$
\succnsim

$\succsim$
\succsim

$\thickapprox$
\thickapprox

$\thicksim$
\thicksim

$\triangleq$
\triangleq

Arrows

$\circlearrowleft$
\circlearrowleft

$\circlearrowright$
\circlearrowright

$\curvearrowleft$
\curvearrowleft

$\curvearrowright$
\curvearrowright

$\downdownarrows$
\downdownarrows

$\downharpoonleft$
\downharpoonleft

$\downharpoonright$
\downharpoonright

$\hookleftarrow$
\hookleftarrow

$\hookrightarrow$
\hookrightarrow

$\leftarrow$
\leftarrow

$\Leftarrow$
\Leftarrow

$\leftarrowtail$
\leftarrowtail

$\leftharpoondown$
\leftharpoondown

$\leftharpoonup$
\leftharpoonup

$\leftleftarrows$
\leftleftarrows

$\leftrightarrow$
\leftrightarrow

$\Leftrightarrow$
\Leftrightarrow

$\leftrightarrows$
\leftrightarrows

$\leftrightharpoons$
\leftrightharpoons

$\leftrightsquigarrow$
\leftrightsquigarrow

$\Lleftarrow$
\Lleftarrow

$\longleftarrow$
\longleftarrow

$\Longleftarrow$
\Longleftarrow

$\longleftrightarrow$
\longleftrightarrow

$\Longleftrightarrow$
\Longleftrightarrow

$\longmapsto$
\longmapsto

$\longrightarrow$
\longrightarrow

$\Longrightarrow$
\Longrightarrow

$\looparrowleft$
\looparrowleft

$\looparrowright$
\looparrowright

$\Lsh$
\Lsh

$\mapsto$
\mapsto

$\multimap$
\multimap

$\nLeftarrow$
\nLeftarrow

$\nLeftrightarrow$
\nLeftrightarrow

$\nRightarrow$
\nRightarrow

$\nearrow$
\nearrow

$\nleftarrow$
\nleftarrow

$\nleftrightarrow$
\nleftrightarrow

$\nrightarrow$
\nrightarrow

$\nwarrow$
\nwarrow

$\rightarrow$
\rightarrow

$\Rightarrow$
\Rightarrow

$\rightarrowtail$
\rightarrowtail

$\rightharpoondown$
\rightharpoondown

$\rightharpoonup$
\rightharpoonup

$\rightleftarrows$
\rightleftarrows

$\rightleftharpoons$
\rightleftharpoons

$\rightrightarrows$
\rightrightarrows

$\rightsquigarrow$
\rightsquigarrow

$\Rrightarrow$
\Rrightarrow

$\Rsh$
\Rsh

$\searrow$
\searrow

$\swarrow$
\swarrow

$\twoheadleftarrow$
\twoheadleftarrow

$\twoheadrightarrow$
\twoheadrightarrow

$\upharpoonleft$
\upharpoonleft

$\upharpoonright$
\upharpoonright

$\upuparrows$
\upuparrows

Relation symbols miscellaneous

$\backepsilon$
\backepsilon

$\because$
\because

$\between$
\between

$\blacktriangleleft$
\blacktriangleleft

$\blacktriangleright$
\blacktriangleright

$\bowtie$
\bowtie

$\dashv$
\dashv

$\frown$
\frown

$\in$
\in

$\mid$
\mid

$\models$
\models

$\ni$
\ni

$\nmid$
\nmid

$\notin$
\notin

$\nparallel$
\nparallel

$\nshortmid$
\nshortmid

$\nshortparallel$
\nshortparallel

$\nsubseteq$
\nsubseteq

$\nsubseteqq$
\nsubseteqq

$\nsupseteq$
\nsupseteq

$\nsupseteqq$
\nsupseteqq

$\ntriangleleft$
\ntriangleleft

$\ntrianglelefteq$
\ntrianglelefteq

$\ntriangleright$
\ntriangleright

$\ntrianglerighteq$
\ntrianglerighteq

$\nvdash$
\nvdash

$\nVdash$
\nVdash

$\nvDash$
\nvDash

$\nVDash$
\nVDash

$\parallel$
\parallel

$\perp$
\perp

$\pitchfork$
\pitchfork

$\propto$
\propto

$\shortmid$
\shortmid

$\shortparallel$
\shortparallel

$\smallfrown$
\smallfrown

$\smallsmile$
\smallsmile

$\smile$
\smile

$\sqsubset$
\sqsubset

$\sqsubseteq$
\sqsubseteq

$\sqsupset$
\sqsupset

$\sqsupseteq$
\sqsupseteq

$\supset$
\supset

$\Supset$
\Supset

$\supseteq$
\supseteq

$\supseteqq$
\supseteqq

$\supsetneq$
\supsetneq

$\supsetneqq$
\supsetneqq

$\subset$
\subset

$\Subset$
\Subset

$\subseteq$
\subseteq

$\subseteqq$
\subseteqq

$\subsetneq$
\subsetneq

$\subsetneqq$
\subsetneqq

$\therefore$
\therefore

$\trianglelefteq$
\trianglelefteq

$\trianglerighteq$
\trianglerighteq

$\varpropto$
\varpropto

$\varsubsetneq$
\varsubsetneq

$\varsubsetneqq$
\varsubsetneqq

$\varsupsetneq$
\varsupsetneq

$\varsupsetneqq$
\varsupsetneqq

$\vartriangle$
\vartriangle

$\vartriangleleft$
\vartriangleleft

$\vartriangleright$
\vartriangleright

$\vdash$
\vdash

$\Vdash$
\Vdash

$\vDash$
\vDash

$\Vvdash$
\Vvdash

Cumulative operators

$\int$
\int

$\oint$
\oint

$\bigcap$
\bigcap

$\bigcup$
\bigcup

$\bigodot$
\bigodot

$\bigoplus$
\bigoplus

$\bigotimes$
\bigotimes

$\bigsqcup$
\bigsqcup

$\biguplus$
\biguplus

$\bigvee$
\bigvee

$\bigwedge$
\bigwedge

$\coprod$
\coprod

$\prod$
\prod

$\smallint$
\smallint

$\sum$
\sum

Punctuations

$.$
.

$/$
/

$|$
|

$,$
,

$;$
;

$\colon$
\colon

$:$
:

$!$
!

$?$
?

$\dotsb$
\dotsb

$\dotsc$
\dotsc

$\dotsi$
\dotsi

$\dotsm$
\dotsm

$\dotso$
\dotso

$\ddots$
\ddots

$\vdots$
\vdots

Escapable symbols

$
$\backslash$ $

$\%$
\%

$\_$
\_

$\}$
\}

$\&$
\&

$\#$
\#

$\{$
\{

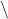Pairing delimiters

$( )$
( )

$[ ]$
[ ]

$\lbrace \rbrace$
\lbrace \rbrace

$\lvert \rvert$
\lvert \rvert

$\lVert \rVert$
\lVert \rVert

$\langle \rangle$
\langle \rangle

$\lceil \rceil$
\lceil \rceil

$\lfloor \rfloor$
\lfloor \rfloor

Nonpairing extensible symbols

$\vert$
\vert

$\Vert$
\Vert

$/$
/

$\backslash$
\backslash

$\arrowvert$
\arrowvert

$\Arrowvert$
\Arrowvert

$\bracevert$
\bracevert

Extensible vertical arrows

$\uparrow$
\uparrow

$\Uparrow$
\Uparrow

$\downarrow$
\downarrow

$\Downarrow$
\Downarrow

$\updownarrow$
\updownarrow

$\Updownarrow$
\Updownarrow

Named operators

$\arccos$
\arccos

$\arcsin$
\arcsin

$\arctan$
\arctan

$\arg$
\arg

$\cos$
\cos

$\cosh$
\cosh

$\cot$
\cot

$\coth$
\coth

$\csc$
\csc

$\deg$
\deg

$\det$
\det

$\dim$
\dim

$\exp$
\exp

$\gcd$
\gcd

$\hom$
\hom

$\inf$
\inf

$\injlim$
\injlim

$\ker$
\ker

$\lg$
\lg

$\lim$
\lim

$\liminf$
\liminf

$\limsup$
\limsup

$\ln$
\ln

$\log$
\log

$\max$
\max

$\min$
\min

$\Pr$
\Pr

$\projlim$
\projlim

$\sec$
\sec

$\sin$
\sin

$\sinh$
\sinh

$\sup$
\sup

$\tan$
\tan

$\tanh$
\tanh

$\varinjlim$
\varinjlim

$\varprojlim$
\varprojlim

$\varliminf$
\varliminf

$\varlimsup$
\varlimsup

Math accents

$\hat{b}$
\hat{b}

$\tilde{b}$
\tilde{b}

$\acute{b}$
\acute{b}

$\bar{b}$
\bar{b}

$\breve{b}$
\breve{b}

$\check{b}$
\check{b}

$\dot{b}$
\dot{b}

$\ddot{b}$
\ddot{b}

$\dddot{b}$
\dddot{b}

$\ddddot{b}$
\ddddot{b}

$\grave{b}$
\grave{b}

$\vec{b}$
\vec{b}

$\widehat{bbb}$
\widehat{bbb}

$\widetilde{bbb}$
\widetilde{bbb}

Math operators

$\int$
\int

$\iint$
\iint

$\iiint$
\iiint

$\iiiint$
\iiiint

$\idotsint$
\idotsint

Accents and other characters

$\'a$
\’a

$\'e$
\’e

$\'{\i}$
\'{\i}

$\'o$
\’o

$\'u$
\’u

¿
?`

¡
!`

“ ”
“ ”

‘ ’
` ‘

$\~n$
\~n

Some types of fonts

${\rm Roman }$
{\rm Roman }

${\em Enfático}$
{\em Enfático}

${\bf Negrita }$
{\bf Negrita }

${\it Itálica }$
{\it Itálica }

${\sl Slanted }$
{\sl Slanted }

${\sf Sans Serif }$
{\sf Sans Serif }

${\sc Small Caps }$
{\sc Small Caps }

${\tt Typewriter }$
{\tt Typewriter }

$\underline{Subrayado}$
\underline{Subrayado}

Letter sizes

Tiny
{\tiny Tiny}

Script
{\scriptsize Script}

Foot
{\footnotesize Foot}

Small
{\small Small}

Normal
{\normalsize Normal}

large
{\large large}

Large
{\Large Large}

huge
{\huge huge}

Huge
{\Huge Huge}

Powers, subscripts, and superscripts

$x^p$
x^p

$(2^2)^n$
(2^2)^n

$\sin^2(x)$
\sin^2(x)

$a_n$
a_n

$u_{N+1}$
u_{N+1}

$a_i^j$
a_i^j

$\sum_{n=1}^{N}u_n$
\sum_{n=1}^{N}u_n

$x^{n+1}$
x^{n+1}

$2^{2^n}$
2^{2^n}

$x^{\sin (x)+ \cos (x)}$
x^{\sin (x)+ \cos (x)}

$a_{n+1}$
a_{n+1}

$u_{_{N+1}}$
u_{_{N+1}}

$\int_a^b f(x) \, dx$
\int_a^b f(x) \, dx

$u_{ij}$
u_{ij}

Square root

$\sqrt{x+1}$
\sqrt{x+1}

$\displaystyle{ \sqrt[n]{x+\sqrt{x}} }$
\displaystyle{ \sqrt[n]{x+\sqrt{x}} }

$\sqrt[n]{x+\sqrt{x}}$
\sqrt[n]{x+\sqrt{x}}

Fractions and two-level expressions

${x+1 \over x-1}$
{x+1 \over x-1}

$\displaystyle \frac{x+1}{x-1}$
\displaystyle \frac{x+1}{x-1}

${{x+1 \over 3} \over x-1}$
{{x+1 \over 3} \over x-1}

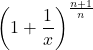
$\displaystyle{\left( 1+ {1 \over x} \right)^{n+1 \over n}}$
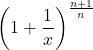
\displaystyle{\left( 1+ {1 \over x} \right)^{n+1 \over n}}

$\displaystyle \left( 1+ \frac{1}{x} \right)^\frac{n+1}{n}$
\displaystyle \left( 1+ \frac{1}{x} \right)^\frac{n+1}{n}

$\displaystyle{\left( 1+ {1 \over x} \right)}^{\displaystyle{n+1 \over n}}$
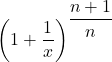
\displaystyle{\left( 1+ {1 \over x} \right)}^{\displaystyle{n+1 \over n}}

${x+1 \brace x-1}$
{x+1 \brace x-1}

${x+1 \brack x-1}$
{x+1 \brack x-1}

Other expressions requiring two levels

$\displaystyle{a \stackrel{f}{\rightarrow} b}$
\displaystyle{a \stackrel{f}{\rightarrow} b}

$\displaystyle{\lim_{ x \rightarrow 0}} f(x)$
\displaystyle{\lim_{ x \rightarrow 0}} f(x)

$\displaystyle{a \choose b}$
\displaystyle{a \choose b}

$\displaystyle{\sum_{\substack{0<i<m\\0<j<n}}a_ib_j}$
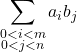
\displaystyle{\sum_{\substack{0<i< m\\0<j<n}}a_ib_j}

$\prod_{\overset{i=0}{i\neq k}}^{n}\frac{w_i}{(w_i-w_k)}$
\prod_{\overset{i=0}{i\neq k}}^{n}\frac{w_i}{(w_i-w_k)}

$L_{n,k}(x) = \prod_{\overset{i=0}{i\neq k}}^{n}\,\frac{x-x_i}{x_k-x_i} = \frac{(x-x_0)(x-x_1)\cdots(x-x_{k-1})(x-x_{k+1})\cdots(x-x_n)}{ (x_k-x_0)\cdots(x_k-x_{k-1})(x_k-x_{k+1})\cdots(x_k-x_n) }$

$$L_{n,k}(x) = \prod_{\overset{i=0}{i\neq k}}^{n}\,\frac{x-x_i}{x_k-x_i} = \frac{(x-x_0)(x-x_1)\cdots(x-x_{k-1})(x-x_{k+1})\cdots(x-x_n)}{ (x_k-x_0)\cdots(x_k-x_{k-1})(x_k-x_{k+1})\cdots(x_k-x_n) }$$

Integral

$\displaystyle{\int_C\boldsymbol{F}\cdot\, dr}$
\displaystyle{\int_C\boldsymbol{F}\cdot\, dr}

$\displaystyle{\oint_C\pmb{F}\cdot\, dr}$
\displaystyle{\oint_C\pmb{F}\cdot\, dr}

$\displaystyle{{\iint_D f(x,y)\,dA}}$
\displaystyle{{\iint_D f(x,y)\,dA}}

$\displaystyle{{\iiint_Q f(x,y,z)\,dA}}$
\displaystyle{{\iiint_Q f(x,y,z)\,dA}}

Adjust delimiters to the size of a formula

$\displaystyle \left[{x+1 \over (x-1)^2} \right]^n$
\displaystyle \left[{x+1 \over (x-1)^2} \right]^n

$\int_{a}^{b}2x\, dx = \left. x^2 \right|_{a}^{b}$
\int_{a}^{b}2x\, dx = \left. x^2 \right|_{a}^{b}

$\displaystyle \left\{ {n \in \N \atop r \neq 1 } \right.$
\displaystyle \left\{ {n \in \N \atop r \neq 1 } \right.

Matrices

$\begin{matrix} 1 & 2 & 3\\4 & 5 & 6\end{matrix}$
\begin{matrix} 1 & 2 & 3\\4 & 5 & 6\end{matrix}

$\begin{pmatrix} 1 & 2 & 3\\4 & 5 & 6\end{pmatrix}$
\begin{pmatrix} 1 & 2 & 3\\4 & 5 & 6\end{pmatrix}

$\begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6\end{bmatrix}$
\begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6\end{bmatrix}

$\begin{Bmatrix} 1 & 2 & 3\\4 & 5 & 6\end{Bmatrix}$
\begin{Bmatrix} 1 & 2 & 3\\4 & 5 & 6\end{Bmatrix}

$\begin{vmatrix} 1 & 2 & 3\\4 & 5 & 6\end{vmatrix}$
\begin{vmatrix} 1 & 2 & 3\\4 & 5 & 6\end{vmatrix}

$\begin{Vmatrix} 1 & 2 & 3\\4 & 5 & 6\end{Vmatrix}$

\begin{Vmatrix} 1 & 2 & 3\\4 & 5 & 6\end{Vmatrix}

$\begin{smallmatrix} 1 & 2 & 3\\4 & 5 & 6\end{smallmatrix}$
\begin{smallmatrix} 1 & 2 & 3\\4 & 5 & 6\end{smallmatrix}

$\begin{pmatrix} D_1t&-a_{12}t_2&\dots&-a_{1n}t_n\\ -a_{21}t_1&D_2t&\dots&-a_{2n}t_n\\\hdotsfor[2]{4}\\-a_{n1}t_1&-a_{n2}t_2&\dots&D_nt\end{pmatrix}$
\begin{pmatrix} D_1t&-a_{12}t_2&\dots&-a_{1n}t_n\\ -a_{21}t_1&D_2t&\dots&-a_{2n}t_n\\\hdotsfor[2]{4}\\ -a_{n1}t_1&-a_{n2}t_2&\dots&D_nt\end{pmatrix}